Non-parametric Bayesian Networks

Non-parametric Bayesian Networks (NPBN), also called copula-based Bayesian Networks or Gaussian copula-based Bayesian Networks, are high-dimensional probability distributions composed of a Directed Acyclic Graph (DAG) with nodes and arcs. Nodes represent random variables while arcs represent the direct qualitative dependence between the linked variables. Panel (a) of the Figure below shows an example of a DAG. Panels (b) and (c) show examples of graphs that do NOT meet the conditions to be a DAG.

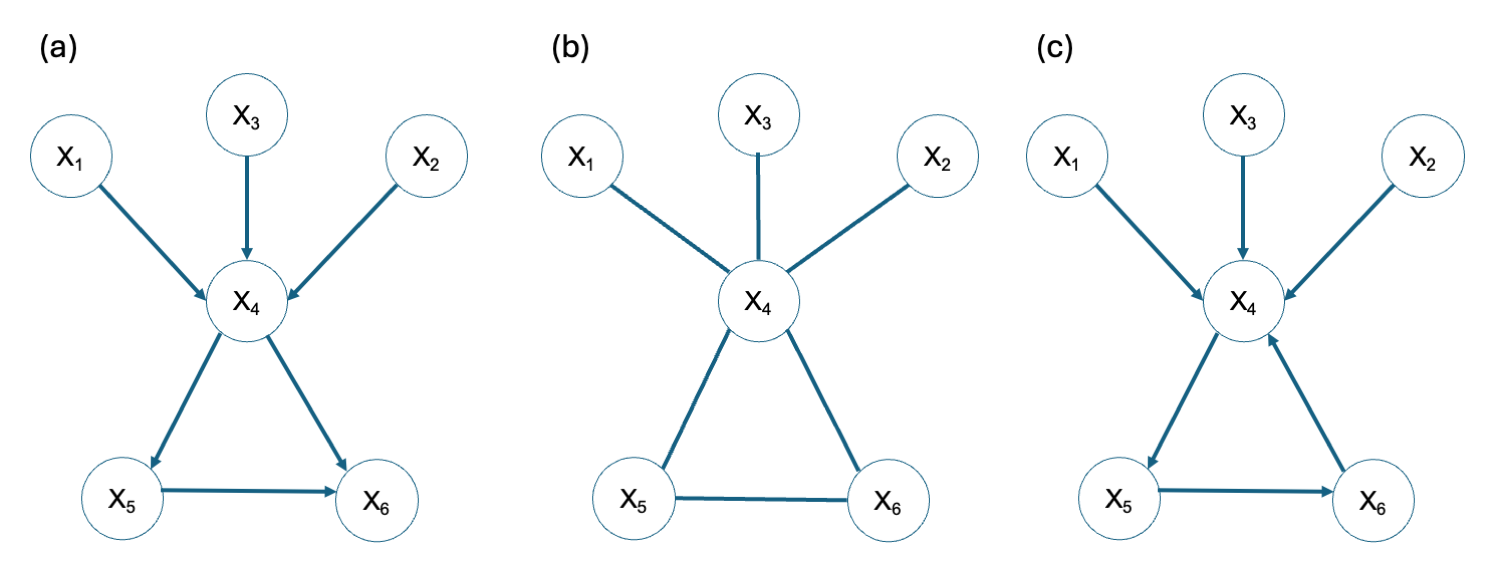
Fig. 8 Examples of graphs: (a) Directed Acyclic Graph, (b) non-Directed Acyclic Graph, and (c) Directed Graph with cycles.

Two nodes linked by an arc are called parent and child, being the parent node the predecessor of the child node. For instance, in panel (a) of the Figure above, \(X_5\) is the parent of \(X_6\) and the child of \(X_4\). Also, nodes preceding the parent nodes are called ancestors. This is, \(X_3\) is the ancestor of \(X_5\) and \(X_6\).

The nodes in the DAG are quantified using univariate distribution, which can be either empirical or parametric of any family, as long as it is invertible. The arcs in the DAG are quantified using bivariate Gaussian copulas with conditional or unconditional rank correlations (further explanation later in this chapter). Thus, the joint distribution is built in bivariate pieces of dependence.

Note that since the dependence between each bivariate pair is modelled using a bivariate Gaussian copula, NPBN have the intrinsic limitations of this copula family. Gaussian copulas are symmetric models which cannot model tail dependence. Therefore, NPBN do not account for tail dependence too.

Conditional correlation intuitively

To begin with the definition of conditional correlation, lets start with only three variables. One conditional correlation then is, intuitively, the correlation of two random variables \(X_1\) and \(X_2\) given a value of a third random variable \(X_3\). Let’s see it with an example. Imagine that you have taken 7 samples of water from a lake and you are investigating the relationship between the temperature of the water, the dissolved oxygen and the concentration of Chlorophyll, as it is an indicator of the amount of algae. In the table below, you have the mentioned observations.

\(X_1\): water temperature (\(^{\circ} C\))	\(X_2\): Chlorophyll a (\(mg/m^3\))	\(X_3\): Dissolved oxygen (\(g/m^3\))
6.1	7.1	10.4
6.8	8.3	8.5
6.3	7.7	8.3
6.1	7.6	11.1
7.0	11.3	12.0
6.1	10.1	11.9
6.2	8.2	10.6

You want to assess the influence of the dissolved oxygen into the concentration of Chlorophyll a, so you compute Pearson’s correlation coefficient as

\[ \rho_{23} = \frac{Cov(X_2, X_3)}{\sigma_{X_2}\sigma_{X_3}} = 0.61 \]

Therefore, it can be concluded that there is a positive correlation between the two random variables. This is, higher values of \(X_2\) are usually associated to high values of \(X_3\).

However, as algae are living organisms, they are sensitive to temperature. Thus, you also compute Pearson’s correlation coefficient between the two variables given that the temperature \(X_1 = 6.1 ^{\circ} C\). To do so, you only consider the first, forth and sixth row of the previous table and compute Pearson’s correlation coefficient, obtaining

\[ \rho_{23|1=6.1} = 0.95 \]

\(\rho_{23|1=6.1}\) is a conditional correlation, which can be very different to \(\rho_{23}\), as seen in the previous example.

Formal definition of conditional and partial correlations

As introduced, conditional correlation is defined as the correlation between two variables given a fixed value of one or more other variables. It is mathematically defined as

\[ \rho_{12|3,...,n} = \rho_{X_1,X_2|X_3=x_3,...,X_n=x_n} = \frac{\mathbb{E} \left( X_1|X3,..., X_n \times X_2|X_3,..., X_n\right)-\mathbb{E}(X_1|X_3,...,X_n)\times \mathbb{E}(X_2|X_3,..., X_n)}{\sqrt{Var(X_1|X_3,..., X_n) \times Var(X_2|X_3,..., X_n)}} \]

Note the similarities with the definition of correlation coefficient.

A partial correlation is the correlation between two random variables whilst taking away the effect of other variables in their relationship. The mathematical definition of partial correlation is given by

\[ \rho_{12;3,...,n} = \frac{\rho_{12;4, ..., n}-\rho_{13;4,...,n} \times \rho_{23;4,...,n}}{\left((1 - \rho^2_{13;4,...,n}) \times (1-\rho^2_{23;4,...,n}) \right)^{1/2}} \]

Only for the Multivariate Gaussian distribution, the partial and conditional correlations are equal, so we can take advantage of that property and write

\[ \rho_{12|3,...,n} = \frac{\rho_{12|4, ..., n}-\rho_{13|4,...,n} \times \rho_{23|4,...,n}}{\left((1 - \rho^2_{13|4,...,n}) \times (1-\rho^2_{23|4,...,n}) \right)^{1/2}} \]

This expression will be later use in the protocol to formally quantify the NPBN.