Correlations in NPBNs

Correlations in NPBNs#

Each Directed Acyclic Graph (DAG) with conditional or unconditional correlations on the arcs can be represented by a rank correlation matrix. In this section, the definition of rank correlation matrix, the semantics of the DAGs and their implication in the representative rank correlation matrix are discussed.

Rank correlation matrix#

A rank correlation matrix representing a DAG with conditional or unconditional correlations is a \(n \times n\) matrix, where \(n\) represents the number of nodes in the DAG. Each element is a rank correlation computed between the random variables whose indexes correspond to the indexes of the rows and columns. This is, a rank correlation matrix for a 4-dimensions problem is given by

\[\begin{split} \begin{pmatrix} r_{11} \ r_{12} \ r_{13} \ r_{14} \\ r_{21} \ r_{22} \ r_{23} \ r_{24} \\ r_{31} \ r_{32} \ r_{33} \ r_{34} \\ r_{41} \ r_{42} \ r_{43} \ r_{44} \end{pmatrix} = \begin{pmatrix} 1 \ r_{12} \ r_{13} \ r_{14} \\ r_{21} \ 1 \ r_{23} \ r_{24} \\ r_{31} \ r_{32} \ 1 \ r_{34} \\ r_{41} \ r_{42} \ r_{43} \ 1 \end{pmatrix} \end{split}\]

The rank correlation computed between one random variable and itself is equal to one. Thus, the diagonal of the rank correlation matrix is populated with 1. Also, it should be noted that the rank correlation matrix is symmetric as \(r_{12} = r_{21}\).

Note that it is also possible to compute a rank correlation matrix from observations. This is, just calculating the rank correlations between each pair of variables based on the observations and putting it in matricial shape.

“How do I want my rank correlation matrix of the DAG to be?”

When deriving a rank correlation matrix from a DAG that we have defined, we get the rank correlations that we are imposing between the random variables that we are studying. Therefore, we would like that those rank correlations are similar to those that we observed in our dataset. The comparison of the rank correlation matrix that we compute from the observations and that derived from the DAG gives us an idea of how good is our model.

You will see more on this topic in section on assessment and validation.

Assigning correlations to the arcs#

Each arc in the DAG is quantified through a conditional or unconditional rank correlation. But how do we assign them?

Consider that each node \(i\) represents a variable \(X_i\). \(Pa(i)={i_1, ..., i_{p(i)}}\) is the set of parent nodes of the node \(i\). The rank correlations associated the arcs \(i_{p(i)-k} \to i\) are given by

(1)#\[\begin{split} \begin{cases} r_{i,i_{p(i)}} & \text{$k=0$}\\ r_{i,i_{p(i)-k}|i_{p(i)},...,i_{p(i)}-k+1} & \text{$1 \leq k \leq p(i)-1$}\\ \end{cases} \end{split}\]

Note that ordering is not unique!

Let’s see how we assign conditional and unconditional rank correlations with an example. Imagine we want to assign the appropriate rank correlations to the DAG in the figure below. We start identifying the partners of each node. The nodes \(X_1\), \(X_2\) and \(X_3\) do not have any parents. \(X_4\) has as parents \(X_1\), \(X_2\) and \(X_3\) so \(Pa(4)=\{1, 2, 3\}\).

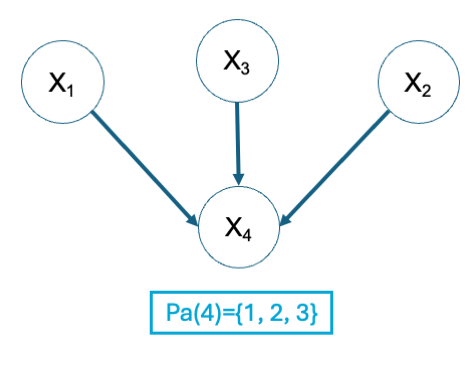
../_images/rank_corr_DAG_empty.png

Fig. 9 Example DAG to assign (un)conditional rank correlations in the arcs.#

Following the previous assignment rule, we start assigning \(r_{34}\) (\(k=0\)) to the arc \(3 \to 4\). Next, for \(k=1\), we assign \(r_{42|3}\) in the arc \(2 \to 4\). Finally, for \(k=2\), we assign \(r_{41|3,2}\) in the arc \(1 \to 4\).

It should be noted that we could have started by other nodes or follow a different order, leading to a different assignment of (un)conditional rank correlations in the arcs and, thus, different non-parametric Bayesian Networks. Although the final joint distribution is slightly different, differences are usually not significant.

In the figure below, the assignment of (un)conditional rank correlations is shown for three different orderings. Note that even more ordering options are possible.

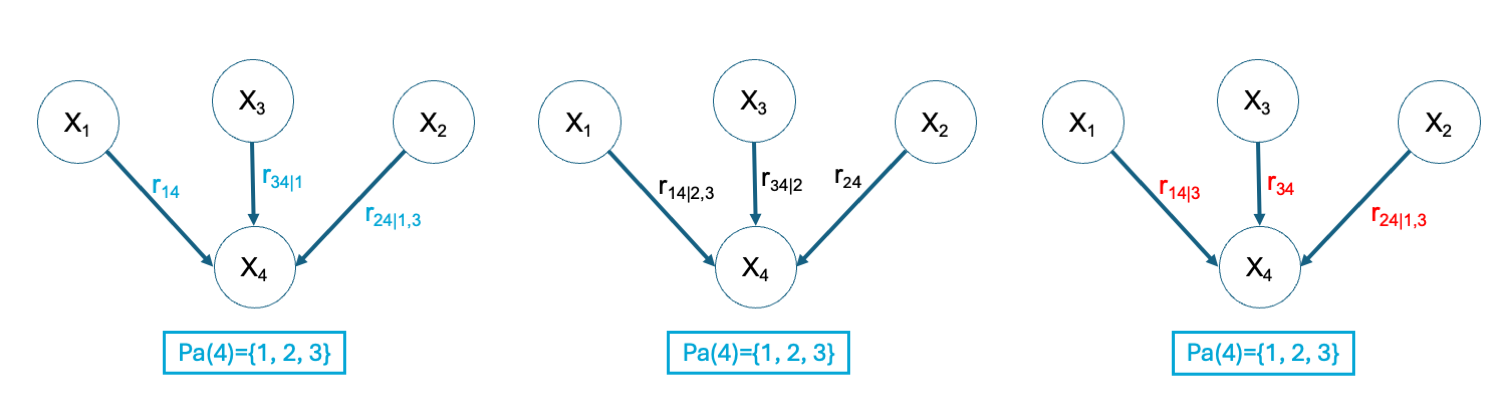
../_images/rank_corr_DAG.png

Fig. 10 Examples of (un)conditional rank correlations assigned to the arcs of a DAG with different orderings.#

This assignment of (conditional) rank correlations for \(i=1,...,n\) results in associating a rank correlation to each arc between parent and child. The following theorem from Hanea et al. (2015)[1] shows that these assignments are independent and uniquely determine the joint distribution for a particular choice of copulae.

Theorem

Given:

  • a directed acyclic graph with n nodes specifying conditional independence relationships in an BN;

  • n variables \(X_1, ..., X_n\) assigned to the nodes, with invertible distribution functions \(F_1, ..., F_n\);

  • the specification (1), \(i=1,...n\), of (conditional) rank correlations on the arcs of the BN;

  • any copula realizing all correlations [-1,1];

  • the (conditional) independent copula realizing all (conditional) independence relationships encoded by the graph of the BN;

the joint distribution of the \(n\) variables is uniquely determined. This joint distribution satisfies the conditional rank correlations in the above expression are algebraically independent and the characteristic factorization given by

\[ f_{1,...,n}(x_1,..., x_n) = f_1(x_1)\prod_{i=2}^n f_{i|Pa(i)}(x_i|x_{Pa(i)}) \]

The fact that the rank correlations are algebraically independent is needed to guarantee that the joint distribution of the \(n\) variables exists and is uniquely determined. This is, not every assignment of rank correlation matrices in the arcs leads to a valid rank correlation matrix.

It’s your turn now!#

Assign the appropriate (un)conditional rank correlations to the DAG in the Figure below.

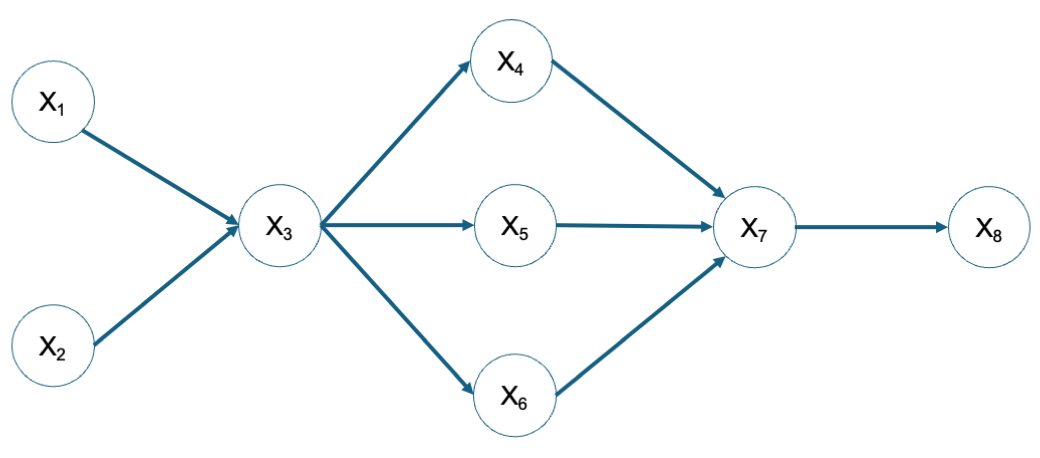
../_images/non_Assigned_ranks.png

Fig. 11 Assign the appropriate correlations.#

Solution

Here the solution for one ordering is provided. Note that this is not the only possible solution.

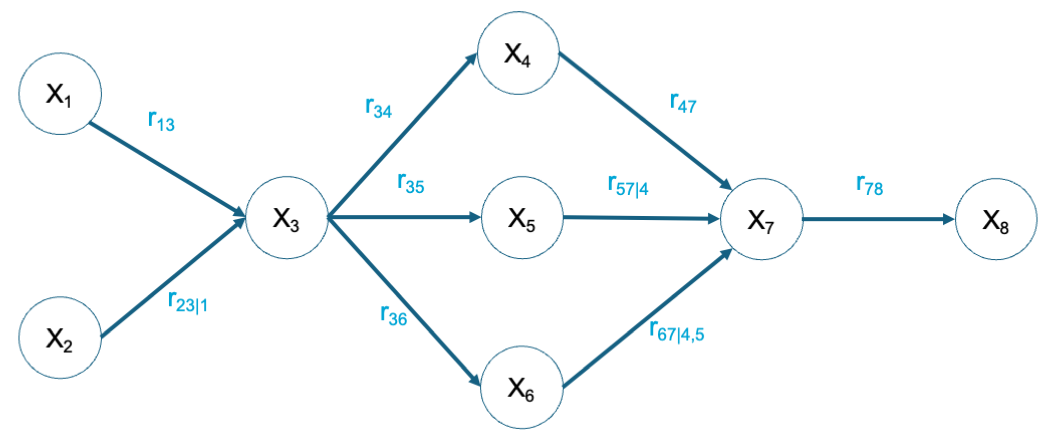
solution

.